Пересечение прямой линии с плоскостью. Определение видимости прямой

Здравствуйте друзья! Сегодня разбираем тему из начертательной геометрии – пересечение прямой линии с плоскостью и определение видимости прямой.

Задание берем из сборника Боголюбова, 1989 год, стр. 63, вар. 1. Нам требуется по заданным координатам построить комплексный чертеж треугольника ABC и прямой MN. Найти точку встречи (пересечения) прямой  с непрозрачной плоскостью ABC.Определить видимые участки прямой.

Пересечение прямой линии с плоскостью

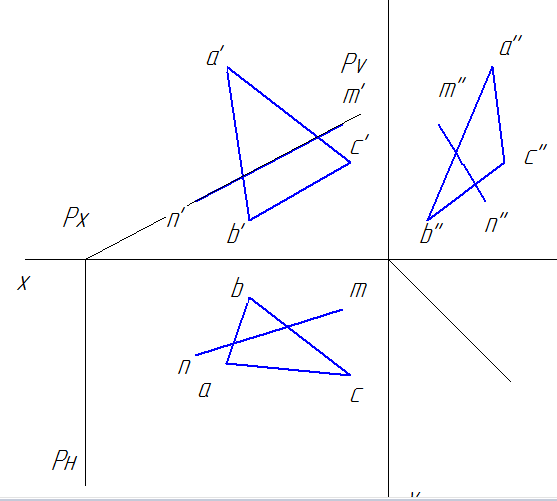
1.  По координатам точек A, B и C строим комплексный чертеж треугольника и прямой NM. Начинаем чертить с горизонтальной проекции. Координаты точек проекции находим при помощи вспомогательных прямых.

2.  Получаем вот такой комплексный чертеж.

3.  Для определения координат точки пересечения прямой и плоскости выполним следующее.

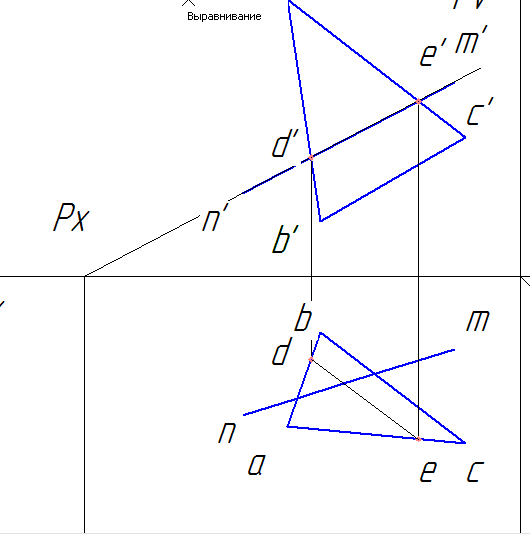
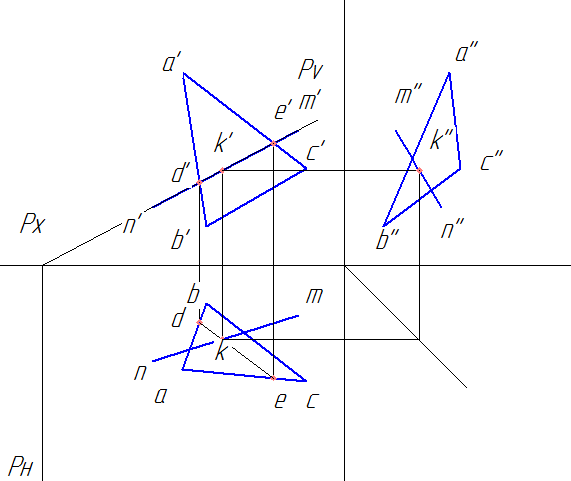
a)  Через прямую NM проводим вспомогательную плоскость Р, т.е. на фронтальной проекции проводим след плоскости Pv, на горизонтальную плоскость опускаем перпендикуляр Рн – горизонтальный след плоскости Р.

b)  Находим фронтальную проекцию линии пересечения следа плоскости Р с треугольником АВС. Это отрезок d’e’. Горизонтальную проекцию находим по линиям связи до пересечения со сторонами ab (т. d) и ac (т. e) треугольника. Точки d и e соединяем.

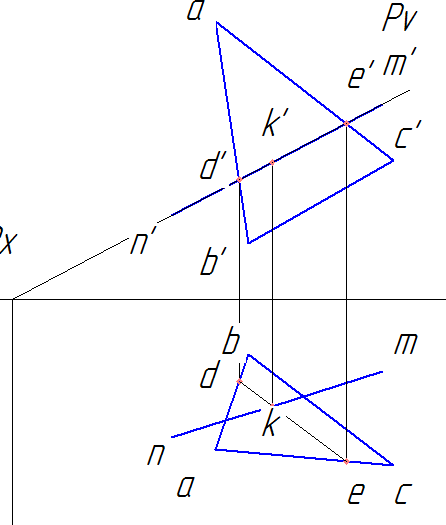
c)  Вместе пересечения de и nm будет находиться горизонтальная проекция искомой точки пересечения прямой линии с плоскостью k.

d)  Проводим линию связи из k до пересечения с d’e’, получаем фронтальную проекцию точки k’.

e)  по линиям связи находим профильную проекцию точки k’’.

Координаты точки пересечения прямой и плоскости К найдены. Эта точка также называется точкой встречи прямой и плоскости.

Определение видимости прямой

Для определения видимости прямой воспользуемся методом конкурирующих точек.

Применительно к нашему чертежу конкурирующими будут точки:

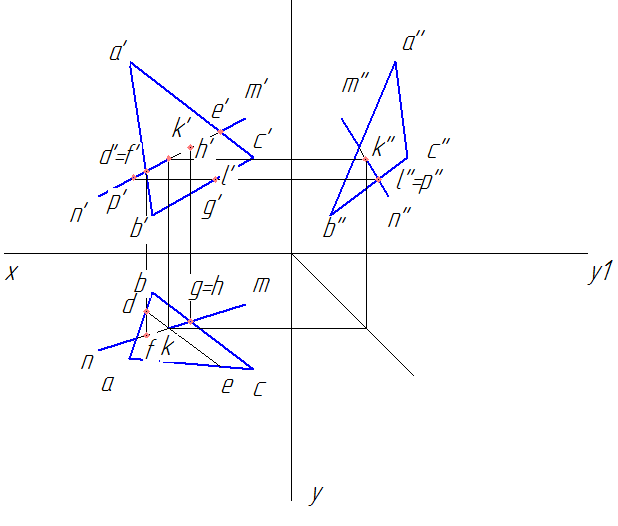
— точки: d’ принадлежащая a’b’  и e’ принадлежащая n’m’ (фронтально конкурирующие),

— точки: g принадлежащая bc  и h принадлежащая nm (горизонтально конкурирующие),

— точки: l’’ принадлежащая b’’c’’  и p’’ принадлежащая n’’m’’ (профильно конкурирующие).

Из двух конкурирующих точек видимой будет та, высота которой будет больше. Граница видимости ограничена точкой К.

Для пары точек d’ и e’ видимость определяем так: опускаем перпендикуляр до пересечения с ab и nm на горизонтальной проекции, находим точки d и f. Видим, что координата по y для точки f больше, чем у d → точка f видима → видима прямая nm на участке f’k’, а на участке k’m’ невидима.

Аналогично рассуждаем и для пары точек g и h: на фронтальной проекции координата по z  у точки h’ больше, чем у g’ → точка h’ видима, g’ – нет → прямая nm на отрезке hk видима, а на участке kn невидима.

И для пары точек l’’p’’: на фронтальной проекции координата по x больше у точки p’, а значит она закрывает собой точку l’’ на профильной проекции → р’’ видима, l’’ нет → отрезок прямой n’’k’’ видим, k’’m’’ невидим.

Заменяем в нужных местах линию nm на невидимую. На этом определение видимости прямой NM на комплексном чертеже треугольника АВС завершено.

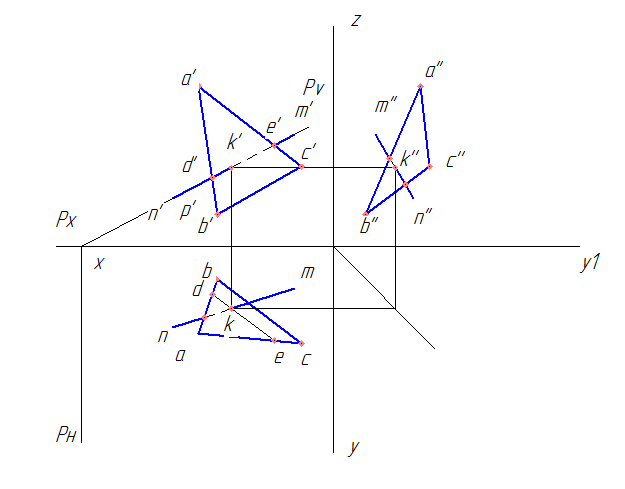
Окончательно чертеж выглядит следующим образом.

Подробно весь процесс построения и определения видимости прямой описан в видеоуроке.

Теперь у вас не вызовет затруднений нахождение точки пересечения прямой линии с плоскостью и определение видимости прямой на проекциях чертежа.